——福建省宁德市教育局薛赞祥

一. 什么是教学重点

虽然我们不能给出一个精确的定义，来描述小学数学教学难点，但是我们可以这样理解：“难点是指学生不易理解的知识或不易掌握的技能技巧。”形成难点的主要原因是，学生原有的认知水平同现有的知识要求之间存在的矛盾。这种矛盾是学生学习新知的障碍，又是发展学生思维能力的有利机会，为此，难点教学既要追求化难为易的过程中发展学生的思维能力。

二. 如何确定教学难点

因为教学难点是学生难学的知识点，所以教师在确定教学难点时，要综合考虑学生的知识基础、经验、能力、思维水平等因素，充分估计学生感到理解困难、推理滞涩、思维容易偏差的知识点。就小学数学教材而言，以下几方面的知识点可确定为教学难点。

1.抽象性的知识点

小学生思维主要依赖于感性的经验，面对不易捉摸、不易想象和不易体验的知识，往往思维受限。如在教学“长方形和正方形的体积”这部分内容时，体积就是一个抽象的概念。如何理解物体所占空间的大小叫它们的体积，对学生说有较大的难度，像这样的知识点就是教学难点。

2.复杂性的知识点

小学生的逻辑思维能力薄弱，面对结构繁杂的知识，往往一筹莫展。如在教学“小数的意义和性质”这部分内容时，小数和复名数的相互改写，学生往往在判别用进率去乘、还是除以进率，小数点向右移、还是向左移的问题出现错误，像这样复杂的知识点就是教学难点。

3.干扰性的知识点

小学生的比较思维能力差，面对结构相似、形式相近的知识点，往往造成混淆不清。如在教学“乘数是两、三位数的乘法”这部分内容时，学生在被乘数、乘数末尾和中间有0的乘法计算中，往往对“0”的处理产生混乱，像这样干扰性的知识点就是教学难点。

4.隐蔽性的知识点

小学生在观察、思考问题时，习惯着眼于表面现象，面对本质特征隐蔽较深的知识，往往容易被表面现象所困扰。如在教学“两步计算的加减应用题”这部分内容时，如何寻找解答两步计算加减应用题隐蔽的“中间问题”，对学生来说是比较困难的，像这样隐蔽性的知识点就是教学难点。

5.特殊性的知识点

小学生的思维惯性较强，面对不同寻常、独具特点的知识点，往往感到疑难困惑。如在教学“带分数加减法”这部分内容时，带分数减法中被减数的分数部分小于减数的分数部分的计算，与以往退位减法的“退一当十”相异，学生就会疑虑重重，像这样特殊性的知识点就是教学难点。

6.陡坡性的知识点

小学生的认知是有序发展的，面对教材中前后联系不紧、思维层次要求不高的知识点，往往容易造成认知脱节。如在教学“20以内进位加法和退位减法”这部分内容时，“9加几的进位加法”与前面教材形成知识表面脱节，造成学生思维活动障碍，像这样陡坡性的知识点就是教学难点。

三.怎样突破教学难点

1.借助直观，简化难点

小学生学习学习抽象性的难点感到困难的主要原因是，缺乏具体的感性经验，为此，教师必须借助直观手段，让学生在观察实验、具体实例中获取丰富的感性认识，建立正确清淅的表象，打好认识基础，达到简化难点的目的。例如，上面讲到“体积”这一难点，教师先引导学生观察火柴盒、砖、保健箱的形式大小，结合实物向学生说明任何物体都占有一定的空间，较大的物体占的空间较大，较小的物体占的空间较小。但空间双是什么呢？看不见、摸不着，为了突破这一思维障碍，教师可进行直观演示，将事先自制的、大小不等的实心橡皮泥长方体分别浸没在两个同样大，盛有等量红色液体的玻璃杯里，让学生直观地看到液面上升，且上升的高度不同，初步感知到什么是物体所占的空间，以及所占空间的大小。这时概括“体积”这一抽象概念，就容易理解了。

2.恰当分散，分化难点

对于复杂性的难点，教师必须采取“恰当分散，各个击破”的方法，设计出若干个逐层深入、一尘环环相扣的教学层次，让学生拾阶而上地解决，达到分化难点的目的。例如，上面讲到“小数和复名数的相互改写”这一难点，教师设计下列三个教学层次：先判断是高级单位化为低级单位，还是由低级单位聚成高级单位，从而决定用进率去乘，还是除以进率。‚确定原有的单位和改写的单位间的进率是多少。ƒ根据乘数确定小数点向什么方向移动，并根据进率确定小数点要移动几位。这样化整为零地分散解决，整个难点也就随之突破了。

3.对比分析，类化难点

干扰性的难点不仅具有鲜明的“个性”，而且存在着很强的“共性”。教师必须采取对比分析的方法，让学生从不同角度、不同层次、不同方面去认识易混知识的异同，达到类化难点的目的。例如，上面讲到“被乘数、乘数末尾有0的乘法”这一难点，学生往往对“被乘数、乘数末尾有0的乘法”与”末尾有0的加减法“（如340×350与340+350 ）对“乘数中间有0的乘法”与”被乘数中间有0的乘法”（如314×601与304×16），产生混淆。对于这些认识失误，必须通过对比分析、比较练习，引起学生的高度注意，以便学生透彻地理解和掌握。

4.揭示本质，内化难点

对于隐蔽性的难点，教师必须精心设计化“隐蔽”为“明显”的教学过程，启迪学生的思维去领悟知识的本质特征，达到内化难点的目的。例如，上面讲到“如何寻找解答两步加减应用题的中间问题”这一难点，在教学课本例一前，先让学生解答：“一辆公共汽车有乘客36人，到胜利街下去18人，这时车上有乘客多少人？”接着补充“又上来9人，这时车上有乘客多少人？”再引导学生理解第一问的计算结果是第二问的一个必要条件，这时将第一部去掉，重新组成一道完整的两步应用题，学生就容易理解隐蔽的“中间问题”了。

5.提前孕伏，淡化难点

特殊性的难点与学生原有的认识结构不相符合，需要重新建构认识结构来理解，因此教师必须做好提前孕伏，调整重组学生认知结构的准备工作的，来顺应新知的学习，达到淡化难点的目的。上面讲到“带分数减法中被减数中被减数的分数部分小于减数的分数部分的计算”这一难点，教学前可先让学生做1-

，引导学生看被减数的分数部分比减数的分数部分小，要从被减数的整数部分拿出1化成假分数，与被减数的分数部分合并起来再减。这样就能使学生顺利地攻克难点了。

6.精心铺垫，同化难点

对于陡坡性的难点，教师就要在学生的已知与未知搭桥铺路，帮助学生唤起头脑中的经验，并与要学习的内容产生联系，使学生主动地把新知牢固地拴在旧知的锚桩上，达到同化难点的目的。例如，上面讲到“9加几的进位加法”这一难点，教师可做如下铺垫：

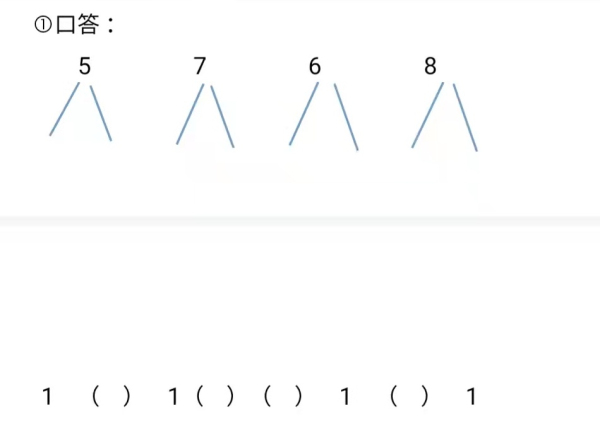
学生答完后，教师再引导学生观察得出：这些数都可以分成“1”和另一个数。

②、填空：

9+（ ）=10 学生填完后，教师追加一句：“9加1就凑成10，可见9一对好朋友”。

③口算：

9+1+3= 9+1+8= 9+1+6 学生算完后，教师部：“这些加法你们怎么算得这么快？”这样把与“9加几的进位加法”相关的旧知进行准备训练，就有助于学生同化新知了。

编辑：王改平 审核：邢有军